矢沢 久雄 グレープシティ アドバイザリースタッフ
連載の第1回で，コンピュータを構成するICの中に論理演算を行う論理回路が入っていることを説明しました。連載の第2回では，論理演算の用途として，マスク，セット，反転があることを説明しました。ここで疑問に思ってほしいことがあります。それは「どうやらコンピュータは，ハードウエア的に論理演算しかできないようだ。それでも，コンピュータで加減乗除の四則演算ができるのは，なぜだろうか？」ということです。実はコンピュータは，論理演算を組み合せて四則演算を行うのです。今回は，その仕組みを説明しましょう。
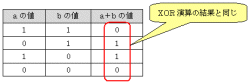
| 表1●2進数の加算結果（その1） |
|
●シンプルな半加算回路
コンピュータは，内部的にすべてのデータを2進数で取り扱います。そこで，2進数で四則演算を行う方法を考えてみましょう。まずは加算からです。2進数の1けた（0または1）で加算を行うと，その結果は表1[拡大表示]のようになります。ここではけた上がりを考えていません。1＋1の結果は10ですが，下位けたは0なので，1＋1＝0としています。表1に見覚えがありませんか？ そうです。XOR演算の真理値表と同じです。すなわち2進数1けたの加算結果は，XOR演算で求められるのです。
| 表2●2進数の加算結果（その2） |
|
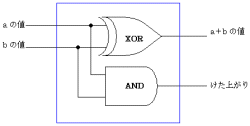
| 図1●半加算回路 |
|
●下位けたからのけた上がりも考えた全加算回路
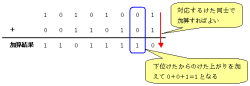
| 図2●8ビットの2進数を加算する例 |
|
全加算回路の3つの入力と演算結果を表3に示します。cは下位けたからのけた上がりです。表3をよく見て，a＋b＋cとそのけた上がりがどのような論理演算の組み合せで表せるか考えてください。
表3●2進数の加算結果（その3）
| aの値 | bの値 | cの値 | a＋b＋cの値 | けた上がり |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
こう言うことは，難しく考えないことです。冷静になりましょう。表3のa＋b＋cの値は表2のa＋bの値と同じくけた上がりを考えていません。そこでa＋b＋cの値は，「aとbの加算結果にcを加算する」すなわち「aとbのXOR演算の結果と，cをXOR演算する」と言えます。したがって論理演算を以下のように組み合わせればよいのです。
a＋b＋c＝（a XOR b）XOR c
表3のけた上がりは，「a，b，cの中で1であるものが少なくとも2つある」すなわち「aとbが1，またはaとcが1，またはbとcが1」と言えます。したがって論理演算を以下のように組み合わせればよいのです。右辺の末尾にOR（a AND b AND c）も加えるべきだと思われるかもしれませんが，a AND b AND cすなわちa，b，cがすべて1なら（a AND b）OR（a AND c）OR（b AND c）のカッコ内のどれかに一致するので，OR（a AND b AND c）を書く必要はないのです。正しい結果が得られるなら，無駄な論理演算を追加するべきではありません。
けた上がり＝（a AND b）OR（a AND c）OR（b AND c）
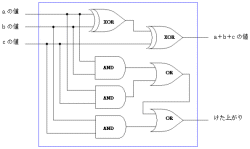
| 図3●全加算回路 |
|
●その他の演算はどうするか？
加算以外の演算（減算，乗算，除算）は，どのように実現したらよいでしょうか？考えただけでも頭が痛くなりそうですね。でも心配は無用です。コンピュータは，補数を使うことでマイナスの値を表すので，補数の加算で減算を実現できます。補数は，もとの値を反転して1を加えることで実現できるので，aというデータの補数は，（NOT a）＋1（補数についてはこちらで詳しく説明しています）となります。乗算は，加算の繰り返しで実現できます。例えば，2×3は，2を3回加算するのと同じです。除算は，減算の繰り返しで実現できます。例えば，10÷2は，10から2が何回引けるかをカウントするのと同じです。これで，四則演算すべてが論理演算で実現できることをご理解いただけましたね。
論理演算の用途である，マスク，セット，反転といった知識は，実際のプログラミングなどでも大いに役に立ちます。それに対して，今回説明した半加算回路や全加算回路は，それを知ったからといって何かの役に立つわけではありません。とは言え，こういう知識を得ると，コンピュータをより身近に感じられるようになるはずです。次回は，「ド・モルガンの法則」を説明します。お楽しみに！
