矢沢久雄
2進数の0と1しか取り扱えないコンピュータは，小数を表すためにトリッキーな方法を使っています。この方法は，浮動小数形式（ふどうしょうすうてんすうけいしき）と呼ばれ，IEEE（アイ・トリプル・イー，Institute of Electrical and Electronics Engineers＝米国電気電子技術者協会）で規定されています。すなわち，トリッキーとはいえ，浮動小数形式が事実上の世界標準なのです。皆さんが，コンピュータのキーボードから3.14のような小数を入力すると，コンピュータの内部では浮動小数形式の情報として表されます。
●固定小数形式と浮動小数形式
|
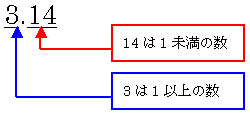
| 図1●固定小数点数形式 |
このような表現方法を「固定小数形式（こていしょうすうてんすうけいしき）」と呼びます。小数点の位置が，その左右で1より大きいかどうかを表す固定的な境目となっているからです。
|
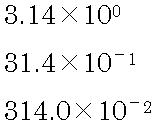
| 図2●浮動小数点数形式 |
浮動小数形式では，「○○×△△の□□乗」というスタイルで小数を表します。このスタイルでは，同じ小数を様々な表現で表すことができます。例えば，3.14という数は，3.14×100，31.4×10－1，314.0×10－2，…などの様々な表現で表せます。これら3つの表現を見比べて分かるように，小数点の位置が変化できるから「浮動（固定でない）」というわけです。
●固定小数形式の2進数
コンピュータでは，浮動小数点形式の2進数で小数を取り扱っています。それに関しては，後で説明しますので，まずはお遊びとして（ドットが使えるとして）固定小数形式の2進数について考えてみましょう。まず問題です。0.1という2進数は，10進数でいくつになるか分かりますか？
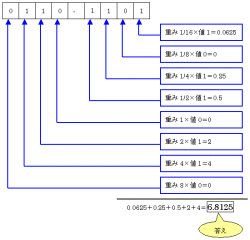
答えは，0.5です。2進数では桁が上がると，重みが2倍されていきます。逆に考えれば，桁が下がると，重みが1/2倍になります。この重みと桁の数である1を掛けて，答えは0.5になります。
|
| 図3●小数点数でも重みを掛けて足す |
●浮動小数形式の2進数
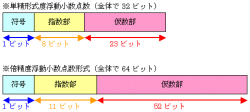
いよいよ本題です。コンピュータは，小数を浮動小数形式の2進数で取り扱っています。0と1だけを使って，「○○×△△の□□乗」というスタイルを表現するために，複数桁の2進数を部分的に分けて使います。どのように分けるかを規定しているのいがIEEEという組織です。「○○×△△の□□乗」の○○の部分を「仮数部（かすうぶ）」と呼びます。△△の部分を「基数部（きすうぶ）」と呼びます。□□の部分を「指数部」と呼びます。基数部は，2進数では2に決まっているので省略し，仮数部，指数部，そして0ならプラス1ならマイナスを意味する符号部を使って小数を表します。複雑なスタイルなので，浮動小数形式では全体を「反転して1」というマイナス表現は使われません。
|
| 図4●単精度浮動小数点数と倍精度浮動小数点数の構造 |
「ぜんぜん分からない」という人もいるかもしれませんね。固定小数形式の2進数も，浮動小数形式の2進数も，それらを理解できないとコンピュータを使う上で困ったことになるわけではありませんので，どうぞ安心してください。ただし，一つだけ知っておいてほしいことがあります。それは，いずれの形式でも2進数で小数が表されているので，10進数のシンプルな小数でも2進数では正確に表せない場合があるということです。
例えば，10進数のシンプルな小数0.1を2進数で表すと0.0001100110011001…という永遠に続く循環小数になります。ICのピンの数に限りがあるコンピュータで永遠に続く循環小数を表すことはできないので，途中で打ち切り，すなわち正確な値が表せないことになります。そのため，小数の計算をコンピュータに行わせると，正確な答えが得られないことがあるのです。これは，事実です。ちょっとだけ計算を間違えるコンピュータって，なかなか可愛いものだと思いませんか。
実は，コンピュータの都合など考えずに，数学の問題として2進数を取り扱うなら，－0110のようにマイナス符号を使ったり，0.011のように固定小数形式を使ってもかまいません。ただし，皆さんは，コンピュータと仲良くなる手段として2進数を学んでいるのです。「マイナスは補数表現で，小数は浮動小数形式だ」と考えてコンピュータに接してください。きっと，いままで気付かなかったコンピュータの本当の姿が見えてくるはずです。次回は，2進数と相性のよい16進数を説明します。
