シミュレーションと再帰で
アルゴリズムの面白さを味わおう
講師 矢沢 久雄
|
|
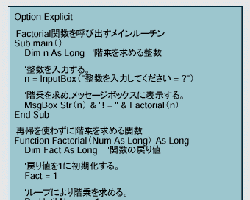
図10●再帰を使わずに階乗を求める関数 このコードは,標準モジュールに記述する |
再帰を利用して階乗を求める
再帰とは,1つの関数の内部からその関数自体を再び呼び出すことである。再帰によって何ができるのかといえば,プログラムを効率的に記述できるということである。もしかしたら,ある関数が呼び出そうとする関数が自分自身であることに,不安を抱く読者もいるかもしれない。だがそんなことはない。理由はこうだ。関数は,プログラム・コードとしてメモリー上に格納されている。メモリーには,あるプログラム・コードがメモリー上のどこにあるか知るために,アドレスと呼ぶ“住所”が振ってある。ある関数はプログラム・コードとして,例えば「C00E10A0」といったアドレスが振ってあるメモリー上から連続して格納してある。
CPUが実行するプログラムの場所は,このアドレスを利用して管理されている。現在実行しているアドレスを示すものを「プログラム・カウンタ」と呼ぶ。関数を呼び出すこととは,その関数のプログラム・コードの開始アドレスにプログラム・カウンタを移すことである。
|
| 写真4●図10の実行結果 |
説明が長くなったが,まずは簡単な問題で再帰の雰囲気をつかんでみよう。
【問題4】パラメータに与えられた数値の階乗を返すFactorial関数を作成せよ。
階乗とは,指定された数から1までの値をすべて掛け合わせたものである。数学では,ある数nの階乗をn!で表し,5!= 5×4×3×2×1= 120となる。階乗は整数の範囲で取り扱われるものであるから,Factorial関数内部で扱うパラメータと,Factorial関数の戻り値は長整数型(Long型)とすればよい。
計算式そのものは単純である。再帰を知らなくとも,図10[拡大表示]のような関数を書けるだろう。ちゃんと動作する(写真4[拡大表示])。なにも間違いはないし,実行して正しい結果を得ることができる。
|
|
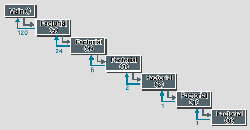
図11●再帰による関数呼び出し 図は5!の場合 |
このアルゴリズムはきれいに再帰に当てはまる。階乗を求める関数の中でパラメータを1だけ小さくして同じ関数をまた呼び出せばよい(図11[拡大表示])。これを繰り返すと,いつかは(n-1)がゼロになる。0!=1と決められているので,その時点で関数の呼び出しが終了し,呼び出された関数は順番に戻り値を返すことになる。
|
|
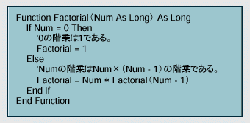
図12●再帰を使って階乗を求める関数 この関数を図10のFactorial関数と差し替えて実行する |
再帰のいいところ,悪いところ
階乗を求めるアルゴリズムには,再帰を利用する手法とそうでない手法があることになる。前者を再帰解と呼び,後者を非再帰解と呼ぶ。階乗に限らず,様々な問題を再帰解または非再帰解のどちらを使っても解くことができる。ここでは,再帰解と非再帰解どちらを利用するべきかの判断のポイントを見てみよう。

|
|
図13●ユークリッドの互除法の非再帰解 このコードは,標準モジュールに記述する |
この連載の第1回では,最大公約数を求めるアルゴリズムとしてユークリッドの互除法を紹介した。与えられた2つの整数mとnの最大公約数を求めるアルゴリズムは,mとnで大きい方から小さい方を引くことを2つの数が等しくなるまで繰り返すというものである。このアルゴリズムをプログラム・コードに置き換える際に,再帰解と非再帰解のどちらを使うこともできる。非再帰解で最大公約数を求める関数GCMを図13[拡大表示]に示そう。
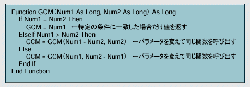
それでは同じアルゴリズムを再帰を使ってプログラム・コードにしてみよう(図14[拡大表示])。再帰を使ったサンプルはこれで2つ目になるが,それらの共通点から何となく再帰の使い方が見えてこないだろうか?
|
|
図14●ユークリッドの互除法の再帰解 この関数を図13のGCM関数と差し替えて実行する |
再帰には問題点が1つある。それは,関数を呼び出すたびに新しいスタック領域が使われるため,何度も再帰を繰り返している内に,スタック不足のエラーが発生する場合があるということだ。スタックはコンピュータのメモリー資源を利用している。これは有限で,再帰による関数呼び出しがあまりに多く繰り返されると,メモリーが足りなくなってコンピュータからエラー・メッセージが表示されることになる。
|
| 写真5●スタック領域の不足によるエラー・メッセージ |
同じパラメータを非再帰解のGCM関数に与えて呼び出してもエラーにはならず,1という正しい答えが得られる。このように,再帰を知ったからといって何でも再帰解で解決しようとするのは危険である。最大公約数を求めるには,非再帰解を使うのが正解だ。





















































