集合論の最も大事な定理の1つに，「ド・モルガンの法則」というのがあります（ド・モルガンの定理とも言います）。これは情報処理技術者試験などでも頻出なのでご存知の方も多いと思いますが，復習を兼ねて改めて書くと，
A, B を集合としたときに，というものです（図1参照。右辺が具体的にどうなるか塗ってみてください）。
1. Not (A∩B) = Not(A) ∪ Not(B)
2. Not (A∪B) = Not(A) ∩ Not(B)
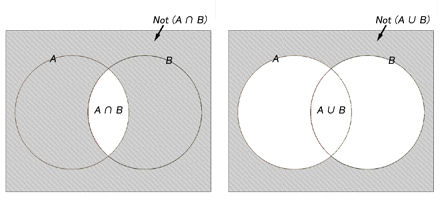
図1●ド・モルガンの法則
さて，
∩は「かつ」とよみ，英語では「AND」，
∪は「または」とよみ，英語では「OR」，
と書くので，上の式は，
1. Not (A AND B) = Not(A) OR Not(B)
2. Not (A OR B) = Not(A) AND Not(B)
ということになります。ここで，世の中のすべての事象は
X または Not(X)
のどちらか一方に排他的に（つまり，片方のみに属し，両方に属するものはない）含まれることを認めるのであれば，X として「A AND B」と置くと，すべての事象は，
A AND B または Not (A AND B) = Not(A) OR Not(B)
のどちらかに含まれるということになります。
さて，ここからITへの応用ですが，例えば，これをSQLの構文に応用するのなら，
Select * From SampleTable Where (A=1 AND B=2)
で取り出したデータと，
Select * From SampleTable Where Not (A=1 AND B=2)
とを合わせると，SampleTableの全レコードを取り出すことができるということになります。ここで，
Where Not (A=1 AND B=2)
のような書き方が文法上許されていないとき（「Not」という演算子が単独で使えない場合など），
「A <> 1」 や 「B <> 2」
を使って上記の式を変形せざるを得ません。
ここで登場するのがド・モルガンの法則で，
Not (A AND B) = Not(A) OR Not(B)
なので，
Where Not (A=1 AND B=2)
は，
Where (A <> 1 OR B <> 2)
と書き直してもいいことが分かります。
もう一度整理すると，
Select * From SampleTable Where (A=1 AND B=2)
で取り出したデータと，
Select * From SampleTable Where (A <> 1 OR B <> 2)
とを合わせると，SampleTableの全レコードを取り出すことができるということになります。
プログラムを読んでいてよく見かけるバグの1つに，上のように，あるデータを2つに分割したいときに「AND」と「OR」が間違っている，というものがあります。この手のバグは，文法エラーでもないし，論理的にも間違っていない，内容が間違っている，という最も見つけにくいバグの1つで，プログラムをする人自身が気をつけないと，修正に非常に時間がかかってしまいます。例として，次を考えてみてください。
よくあるプログラムですが，フィールド "名前" に値が入っているデータのみを抽出するには，
Answer1
Select 名前 from SampleTable
Where ( 名前 <> "" ) OR ( 名前 <> null )
なのか
Answer2
Select 名前 from SampleTable
Where ( 名前 <> "" ) AND ( 名前 <> null )
なのか，どちらが正しいでしょうか？
こういうのを慌てると間違えます。混乱してきたら，逆の場合を考えればいいのです。名前が入っていないときは，( 名前 = "" ) または ( 名前 = null) の2通りのどちらかなので，その「逆」は，「または」の逆 "AND" を使うのが正しいです。つまり，Answer2が正しいです。
プログラムをするときにぜひとも心がけたいことは，
★何かを「AND」で抽出したらそれ以外の部分すべては「OR」で抽出する★
★何かを「OR」で抽出したらそれ以外の部分すべては「AND」で抽出する★
ということです。もっと細かく言うなら，
★「AND」で抽出した以外の部分は，Not をつけて「OR」で抽出する★
★「OR」で抽出した以外の部分は，Not をつけて「AND」で抽出する★
ということです。
応用してみましょう。AND や OR がたくさんある場合，例えば，
Select * From SampleTable
Where (A <> 1 OR B <> 2) AND (C = 3)
の反対は，
Select * From SampleTable
Where (A = 1 AND B = 2) OR (C <> 3)
になります（図2を参照。"反対"部分については下図を塗ってチェックしてみてください）。
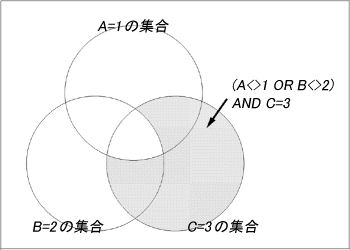
図2●(A <> 1 OR B <> 2) AND C = 3
「AND」を「OR」，「OR」を「AND」に変えて，評価の条件（A<>1など）を反対にする（A<>1 ならば A=1と変更）だけです。
もう1つ大事なポイントは，演算優先順位が，"AND(論理積)"が"OR(論理和)"より先（掛け算のほうが足し算より演算優先順位が高い）ということで，
A OR B AND C は， A OR (B AND C)
だということです。たとえ演算の優先順位を分かっていてもいつでも括弧でくくるようにしてください。
さらに複雑なケースを考えてみましょう。
Select * From SampleTable
Where (A <> 1 OR B <> 2) AND (C = 3 OR D = 4) OR (E = 5 OR F <> 6)
は，
Select * From SampleTable
Where ( (A <> 1 OR B <> 2) AND (C = 3 OR D = 4) ) OR (E = 5 OR F <> 6)
と書き直すことができる(AND が先に計算されるので括弧でくくる)ので，その反対は，
Select * From SampleTable
Where ( (A = 1 AND B = 2) OR (C <> 3 AND D <> 4) ) AND (E <> 5 AND F = 6)
となります。
（誤）Select * From SampleTable
Where (A = 1 AND B = 2) OR (C <> 3 AND D <> 4) AND (E <> 5 AND F = 6)
ではないことに注意してください(AND と OR の演算順位が影響してしまっている）。AND と OR を入れ替えるときに演算の優先順位が入れ替わってしまうので，括弧でくくる必要があるのです。
ということで，長くなってしまいましたが，
★「AND」で抽出した以外の部分は，Not をつけて「OR」で抽出する★
だけ覚えておいてください。
抽出条件が複雑だと図に描くのも大変になってきて考えると頭がこんがらがってしまいますが，上のことだけ知っていれば，考えなくても機械的に条件文が書けてしまうのがド・モルガンの法則のいいところです。
