アルゴリズムと聞いて、何を思い浮かべますか。「実際にプログラミングを行う上では何に役立つかよくわからない」と感じている方もおられるのではないでしょうか? この連載では、「アルゴリズム」を、具体的な問題に対して適用していく際の考え方を紹介します。今回は「8パズル」について解説します。
問題1◆8パズル
この問題を幅優先探索で解くには、「パズルのパネルが最初にどういった配置になっているか」ということを示す初期状態を頂点とし、そこから遷移可能な状態を辺でつないだグラフで表します(図1)。初期状態から辺でつながれた状態を次々に調べることによって、探索を進めていくわけです。
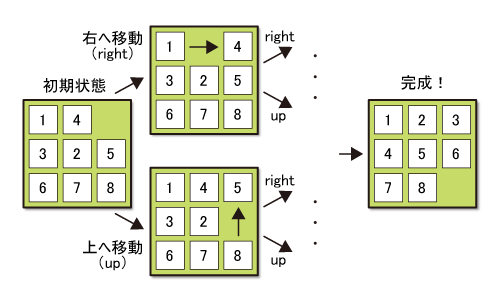
この問題を考える際に、多くの読者が気になるであろうことは、状態の多さでしょう。前回紹介した「川渡り問題」では、状態は72個しか存在しないので、状態の数を気にしなくても、一瞬で計算が終わることがわかりました。
しかし、今回の問題はそうは行きません。かなり多くの数の状態が存在しそうなので、広い範囲にわたって探索をしなければいけない可能性があります。こうしたときに、「いったいどれだけの計算時間が必要か」、「いったいどれだけのメモリーが必要となるのか」を知ることは、プログラムを組む上で非常に重要です。
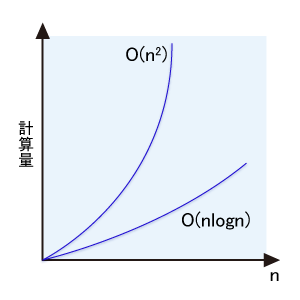
計算量はもともと、扱うデータのサイズが大きくなった際に、必要な実行時間やメモリー使用量がどのように変化するかを考えるためのものです。例えば、n個のデータの並べ替え(ソート)を行うとき、バブルソートはn^2のオーダーの計算量になり、マージソートではnlognのオーダーの計算量になる、といった具合です。これらをそれぞれ、O(n^2)、O(nlogn)と表します。nが小さい場合は、前者の方が計算量が少ないこともありますが、通常は後者の方が圧倒的に計算量が少なくなります(図2)。
今回は大ざっぱに「一番計算が行われる処理の回数を数える」ことによって計算量を見積もることにします。処理の回数が1億回程度であれば、最近のコンピュータでは1、2秒で終了します。
「計算量を把握するためには一番多く処理をする場所を数えればよい」と言われても、それ以外の場所の計算時間を無視して良いのかと心配な人もいるでしょう。そういう人のために、次のようなソースコードを考えてみます。
A();
for(int i=0;i<n;i++){
B();
for(int j=0;j<n;j++){
C();
}
}nが1、10、100、1000、1万のとき、A( )が実行される回数はいずれも1です。これに対してB( )が実行される回数はそれぞれ1、10、100、1000、1万となり、C( )の実行回数は1、100、1万、100万、1億となります。nが大きくなれば大きくなるほど、一番計算回数が多いC( )の実行回数は、ほかに比べてすごい勢いで(O(n^2)で)増えていくのです。従って、ある程度nの数が大きくなったら、一番計算する回数の多い部分だけを考えれば、計算量をほぼ正しく見積もれることがわかります。





















































