皆さんは、アルゴリズムと聞いて、何を思い浮かべますか？ 多くの人は「プログラミングの基礎技術で、学ぶべきもの」という認識を持っていて、実際に書籍などで学習したことのある人も多いでしょう。しかし、一方で「実際にプログラミングを行う上では何に役立つかよくわからない」とも感じているのではないでしょうか？
例えば、アルゴリズムの書籍では様々なソートアルゴリズムが紹介されていますが、一つ覚えてしまえば実用上困らないでしょうし、そもそも大抵の言語にソート関数は標準で用意されています。最短経路問題を解くことができるダイクストラ法は非常に有名なアルゴリズムですが、実際に自分のプログラムで使ったことがある人はほとんどいないのではないでしょうか？
そういった、使いどころが見いだせない「アルゴリズム」を、具体的な問題に対して適用していく際の考え方を紹介しようというのが、この特別連載です。ここでは数あるアルゴリズムのうちで最も適用範囲の高いものの一つ、「幅優先探索」にフォーカスを当てて、どれだけ広い範囲の問題に対して役立つのかを見ていきます。
今回は幅優先探索の基本について解説します。
例題1
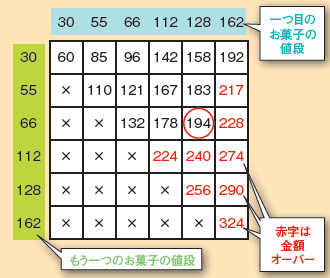
この問題を手で解くとしたら、高い方のお菓子から順番に組み合わせて…、などとやるのでしょうが、コンピュータを使うのであれば非常に簡単です。しらみ潰しに、すべてのお菓子の組み合わせの合計金額を調べてしまえば良いのです。
200円以下で合計金額が一番高くなる組み合わせが答えです（図2）。forループを二つ使えば、プログラムを組むのは非常に簡単だと思います。
しかし、このようなアルゴリズムでは、調べられることは非常に限られます。例えば、同じ前提で3種類のお菓子を買う場合はどうでしょう。forループを三つ書けば良いと言えばそれまでかもしれませんが、個数が増えるたびにforループを増やすのは面倒です。
さらに、問題を拡張してみましょう。
