問題

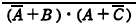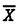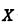問３　論理式と等しいものはどれか。ここで，・は論理積，＋は論理和，はの否定を表す。

ア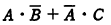　
イ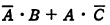　
ウ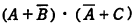　
エ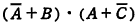　

テクノロジ系>基礎理論>基礎理論>離散数学

解説と解答

　一つ一つの式を確認するよりも，論理演算の法則を利用して式を簡略化して比較します。ここでは，以下の2つの法則を利用します。なお，not(X)は，Xの否定を表します。

●ド・モルガンの法則
not(X・Y)＝not(X)＋not(Y)
　...論理積全体の否定はそれぞれの否定の論理和(1)
not(X＋Y)＝not(X)・not(Y)
　...論理和全体の否定はそれぞれの否定の論理積(2)

●否定の否定の法則
not(not(X))＝X
　...否定の否定は元に戻る(3)

　問題の式に，以上の(1)～(3)の法則をあてはめてみましょう。

　not((not(A)+B)・(A+not(C)))
＝not(not(A)+B)＋not(A+not(C)) ...上記(1)より
＝not(not(A))・not(B) + not(A)・not(not(C)) ...上記(2)より
＝A・not(B) + not(A)・C ...上記(3)より

よって正解は，選択肢アです。

佐塚 彰夫（さづか あきお）
アイティ・アシスト 代表取締役
ITに関するコンサルティングや教育を実施するアイティ・アシストの代表。新人研修やプロジェクトマネージャ育成研修をはじめ，基本情報技術者試験，応用情報技術者試験，プロジェクトマネージャ試験などの試験対策研修の実績も豊富。著書に「短期完全マスター 基本情報技術者 2009年版」などがある。