製品と部品の関連性を明確にしたり,どのような順番で配送先を回るかなど,ビジネスの世界では複数の要素同士の関係性を考えることが多い。そこで今回は,要素を「点」に,関係性を「辺」で表し,その特徴を分析する「グラフ理論」について解説する。
ビジネスの世界では,ある要素と別の要素を関連付けて整理したり,分析することが多い。例えば,部品を効率的に発注するために,複数の製品に共通する部品(要素)を洗い出す場合。また「巡回セールマン問題」のように,商品を複数の地域に配送する際に,各地域(要素)をどのような順番で回れば無駄なく網羅して配送できるかを検討するような場合がある。効率の良い通信網を張り巡らせるためにノードをどう配置するかも同様だ。
要素の数が少なければ,分析は難しくない。しかし要素の数が膨大になっていくと,頭の中だけで考えても答えを導き出せない。そこで有用なのが,各要素間のつながりをグラフで表して分析する「グラフ理論」である。グラフ理論とは現実世界の様々な要素を「点」に置き換え,その関係性を「辺」で結び特徴を分析する手法だ。
意識しているかどうかは別として,グラフ理論のお世話になっているITエンジニアは多いはずだ。身近な活用例には,データを効率的に探索できる「2分探索木」が挙げられる。さらに,データとデータのつながりを示した「リスト構造」もグラフの一種だ。複雑な関係を単純化して分析するグラフ理論は,ITエンジニアにとって欠かすことのできない知識の1つである。
ここではまず,グラフ理論の基礎について説明し,そのうえで実際にグラフを使った様々な問題を見ていこう。
グラフは「点」と「辺」で構成される
一般に,「グラフ」と聞くと棒グラフや折れ線グラフを想像する方が多いだろう。しかし,これらはグラフ理論が対象とするグラフではない。グラフ理論で言う「グラフ」とは,「点」と点同士を結ぶ「辺」から構成される(図1)。
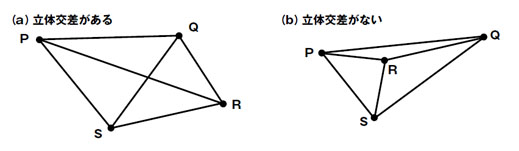 |
| 図1●グラフ理論に基づくグラフの例 グラフは「点」と,点同士を結ぶ「辺」から成る。グラフ理論においては,点の位置や辺の形状・長さは意味を持たない。よって,(a)と(b)のグラフは立体交差の有無の違いはあるが,グラフそのものが示す意味は同じである |
すなわち,グラフは点と点の“つながり方”を表すものだ。個々の点をデータと考えれば,グラフはデータとデータの関係性を表していると言えよう。
ポイントは,グラフ理論では物理的な点の位置や辺の形状などは,どれも問題としていないこと。例えば,図1の(a)と(b)のグラフは形こそ違うものの,グラフが示す意味は同じである。なぜなら,(a)の点Rをつまんで上に持ち上げた状態が(b)のグラフだからだ。
1つの点に付いている辺の数を,「次数(じすう)」と呼ぶ。例えば,図1の(a)と(b)における点Pの次数はどちらも3である。
辺の向きを考えたグラフは「有向グラフ」と呼ぶ(図2)。これに対して図1のように辺の向きを考慮していないグラフを「無向グラフ」と呼ぶ。有向グラフは一方通行の道路のようなもので,辺に矢印を付けることで示される。有向グラフは,点に入ってくる辺の数「入次数(いりじすう)」と,点から出ていく辺の数「出次数(でじすう)」を区別している。図2の例で言えば,点Pの入次数は2で,出次数は1となる。
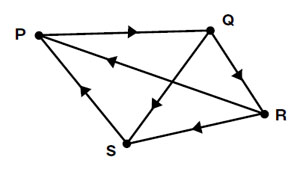 |
| 図2●辺に“向き”を加えた「有向グラフ」の例 辺の向きを考えたグラフが「有向グラフ」である。辺の向きは矢印で示される。辺に向きがないグラフは「無向グラフ」と呼ぶ |
さて,いろいろな用語が出てきたが,ここでグラフの「性質」についても触れておきたい。グラフは必ず,次の2つの性質を備えている。
1つ目の性質は,「あらゆるグラフは,次数の合計が偶数になる」というものだ。なぜなら,1つの辺には2つの点(始点と終点)があるため,次数の合計は必ず「辺の数×2」となるのである。
もう1つの性質は,「あらゆるグラフは,奇数の次数を持つ点が偶数個ある」というものだ。これは1つ目の性質とも関連するが,奇数の次数を持つ点が奇数個あるとしたら,次数の合計は奇数になってしまう。よって,奇数の次数を持つ点は必ず偶数個になるのである。
このようなグラフの性質を利用すると,現実世界の様々な問題を解決できる。以下で,代表的なグラフを使った問題について考えてみよう。





















































