銀行の現金自動預払機(ATM)やテーマパークのアトラクションなど,何かのサービスを待つために行列を作るというのは街中でよく見かけます。このような行列,同じような込み具合でも並び方によって待ち時間が違ってきます。ちょっと不思議な感じがするお話をしましょう。
並び方で待ち時間が変わる
お客さんはランダムに到着し,一人当たりにかかるサービス時間もランダムで,窓口が1個の行列があったとします。ここで,お客さんの数が2倍に増えたため,窓口をもう1個増やして,次のどちらかの方法をとることにしました。方法Aでは窓口ごとに別々の行列を作ります。方法Bではお客さんに1列に並んでもらって,空いた方の窓口を利用してもらいます。実はこれら2種類の並び方によって,お客さんの平均待ち時間が違ってくるのです。検証してみましょう。
まずはそれぞれの窓口の利用率を比較します。方法Aは行列が二つになり,お客さんが2倍になったのだから,利用率は従来通りです。方法Bは窓口が2個になったので単位時間に対応できるお客さんの数は2倍,到着するお客さんの数も2倍と考えることができます。すると,方法Bでも従来の利用率と同じになります。
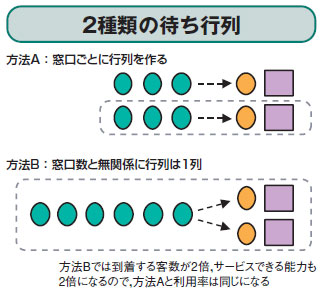 |
| 図1●2種類の待ち行列 |
次に待ち行列の公式を基に作成したグラフを利用して,この二つの行列の待ち時間を比較してみます。すると窓口数2(方法B)の方は,窓口数1(方法A)と比べて,どの利用率でも待ち時間が1/2以下になっているのがわかります。キツネにつままれたような気もしますが,これで間違っていません。長い行列ができるときもあれば,ガラガラのときもあることを考慮すれば実感できるでしょう。
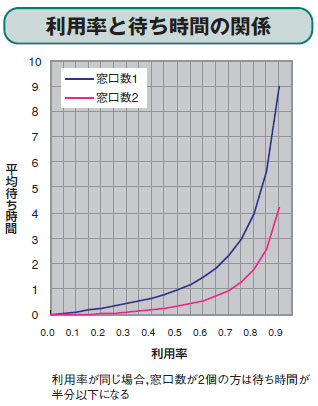 |
| 図2●利用率と待ち時間の関係 |
ケンドールの記法とは
このように,同じ数の窓口があった場合でも,待ち行列の作り方によって待ち時間は変わります。そして,このことはネットワーク設計にも大きくかかわってきます。
数学では待ち行列の形・性質を「アルファベット/アルファベット/数値」で表記します。これをケンドールの記法と呼びます。
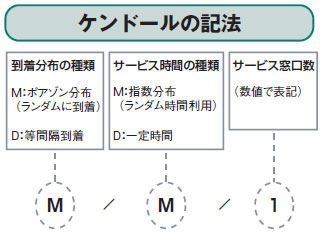 |
| 図3●ケンドールの記法 |
最初のアルファベットは到着間隔のパターンで,Mの場合は到着間隔がランダム(ポアゾン分布に従う),Dの場合は到着間隔が一定という意味になります。真ん中のアルファベットはサービス時間で,Mの場合はサービス時間がランダム(指数分布に従う),Dの場合はサービス時間が一定という意味です。そして最後の数値はサービス窓口の数を意味します。先ほど参照したグラフは,M/M/1とM/M/2を基に作成したものだったのです。
|





















































